Sabe aquele eterno otimista que só vê o lado positivo das coisas?
O módulo é deste jeito.
Brincadeiras à parte, o módulo ou valor absoluto de um número real x é representado por |x|, que lemos: módulo de x.
Se x for um número real positivo o módulo de x será o próprio x.
Se x for um número real negativo o módulo de x será o oposto de x, ou seja, será -x, resultando portanto em um valor positivo.
Apenas sendo x igual a 0, o módulo de x também será 0.
Em resumo temos:
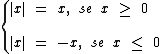 Embora não seja um conceito complexo, vamos ver alguns exemplos. Inicialmente vejamos exemplos bem simples:
Embora não seja um conceito complexo, vamos ver alguns exemplos. Inicialmente vejamos exemplos bem simples:
Exemplo de Módulo de Números Reais
Módulo de um Número Real Positivo
 |17|
Neste exemplo temos um número positivo, já que 17 > 0, então o |17| é igual ao próprio 17, pois
|17|
Neste exemplo temos um número positivo, já que 17 > 0, então o |17| é igual ao próprio 17, pois 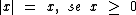 , logo:
, logo:
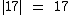
 |17|
|17|Módulo de um Número Real Negativo
 |-17|
Neste outro exemplo temos um número negativo, já que -17 < 0, então o |-17| é igual ao oposto ou simétrico de -17, que é 17, pois
|-17|
Neste outro exemplo temos um número negativo, já que -17 < 0, então o |-17| é igual ao oposto ou simétrico de -17, que é 17, pois 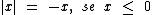 :
:
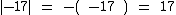
 |-17|
|-17|Módulo de um Número Real Nulo
 |0|
Como
|0|
Como 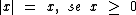 , então
, então 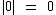 .
Ou por outro lado, como
.
Ou por outro lado, como 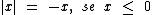 , então
, então 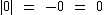 .
.
Agora vamos ver alguns exemplos um pouco mais complexos:
 |x - 5|
Para obtermos o valor do |x - 5| precisamos identificar quando x - 5 ≤ 0 e quando x - 5 ≥ 0.
Ora, se x - 5 ≥ 0 então:
|x - 5|
Para obtermos o valor do |x - 5| precisamos identificar quando x - 5 ≤ 0 e quando x - 5 ≥ 0.
Ora, se x - 5 ≥ 0 então:
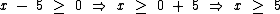 Logo para x ≥ 5 temos x - 5 ≥ 0, portanto segundo a definição do módulo temos:
Logo para x ≥ 5 temos x - 5 ≥ 0, portanto segundo a definição do módulo temos:
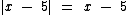 Já para x ≤ 5 temos x - 5 ≤ 0, de onde concluímos que:
Já para x ≤ 5 temos x - 5 ≤ 0, de onde concluímos que:
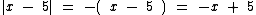 Resumindo temos:
Resumindo temos:
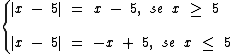
Para finalizarmos os exemplos vamos analisar a sentença |x - 5| + |x - 2| para x ≤ 2, para x ≥ 5 e para 2 ≤ x ≤ 5:
 |x - 5| + |x - 2| para x ≤ 2
Como temos x ≤ 2, então x - 2 ≤ 0, pois para ser maior que 0, seria necessário que x fosse maior que 2.
Analogamente temos x - 5 < 0, pois como x ≤ 2 o maior valor que podemos obter para x - 5 é -3.
Em função disto o |x - 5| será -(x - 5) e o |x - 2| será -(x - 2).
Então temos:
|x - 5| + |x - 2| para x ≤ 2
Como temos x ≤ 2, então x - 2 ≤ 0, pois para ser maior que 0, seria necessário que x fosse maior que 2.
Analogamente temos x - 5 < 0, pois como x ≤ 2 o maior valor que podemos obter para x - 5 é -3.
Em função disto o |x - 5| será -(x - 5) e o |x - 2| será -(x - 2).
Então temos:
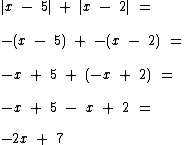
 |x - 5| + |x - 2| para x ≥ 5
Neste outro exemplo como x ≥ 5, então x - 5 ≥ 0 e x - 2 > 0.
Então |x - 5| será x - 5 e o |x - 2| será x - 2.
O que resulta em:
|x - 5| + |x - 2| para x ≥ 5
Neste outro exemplo como x ≥ 5, então x - 5 ≥ 0 e x - 2 > 0.
Então |x - 5| será x - 5 e o |x - 2| será x - 2.
O que resulta em:
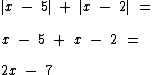
 |x - 5| + |x - 2| para 2 ≤ x ≤ 5
Neste último exemplo temos x - 5 ≤ 0, pois x pode ser no máximo ser igual a 5 e x - 2 ≥ 0, pois o valor mínimo de x é2.
Temos então que o |x - 5| será -(x - 5) e o |x - 2| será x - 2.
E portanto:
|x - 5| + |x - 2| para 2 ≤ x ≤ 5
Neste último exemplo temos x - 5 ≤ 0, pois x pode ser no máximo ser igual a 5 e x - 2 ≥ 0, pois o valor mínimo de x é2.
Temos então que o |x - 5| será -(x - 5) e o |x - 2| será x - 2.
E portanto:
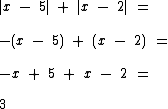
 |0|
|0| |x - 5|
|x - 5| |x - 5| + |x - 2| para x ≤ 2
|x - 5| + |x - 2| para x ≤ 2 |x - 5| + |x - 2| para x ≥ 5
|x - 5| + |x - 2| para x ≥ 5 |x - 5| + |x - 2| para 2 ≤ x ≤ 5
|x - 5| + |x - 2| para 2 ≤ x ≤ 5Propriedades do Módulo de Números Reais
Para quaisquer valores reais de x temos as seguintes propriedades:
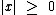
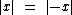
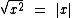
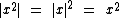 Para a e b reais temos as seguintes propriedades:
Para a e b reais temos as seguintes propriedades:
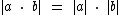
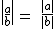 para
para 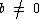
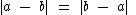
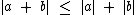 Para
Para 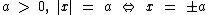 Para
Para 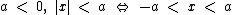 Para
Para 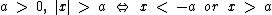
Conceituando Geometricamente o Módulo de um Número Real
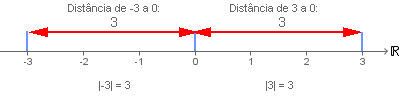 Em termos geométricos o módulo de um número real representa a distância deste número à origem de uma reta real.
Na reta desta figura o ponto 0 representa a suaOrigem. Cada ponto nesta reta é um número real.
Como podemos observar, 3 tanto é a distância do ponto -3 até a origem,quanto é a distância do ponto 3 também até a origem.
A distância dos pontos em questão é igual a 3 nos dois casos, não importando se o ponto está à direita ou à esquerda da origem. O valor absoluto ou módulo de -3 é igual a 3, assim como o módulo de 3 também o é.
Em termos geométricos o módulo de um número real representa a distância deste número à origem de uma reta real.
Na reta desta figura o ponto 0 representa a suaOrigem. Cada ponto nesta reta é um número real.
Como podemos observar, 3 tanto é a distância do ponto -3 até a origem,quanto é a distância do ponto 3 também até a origem.
A distância dos pontos em questão é igual a 3 nos dois casos, não importando se o ponto está à direita ou à esquerda da origem. O valor absoluto ou módulo de -3 é igual a 3, assim como o módulo de 3 também o é.

Solucionando Equações Modulares no Conjunto dos Números Reais

Para encontrarmos os valores de x que tornam esta equação verdadeira, devemos eliminar o módulo e escrever duas equações. Na primeira o segundo membro será o oposto de 11 e na outra será o próprio número 11:
Em relação a estas duas equações não há o que pensar. -11 e 11 são solução da equação 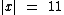 .
.
Se quisermos a resposta na forma de um conjunto, representando por S o conjunto solução, temos:

Solucionemos agora este exemplo não tão óbvio.
Assim como fizemos na caso anterior, vamos eliminar o módulo escrevendo duas equações, sendo que em uma delas inverteremos o sinal do segundo membro.
Basta, portanto, solucionarmos cada uma delas e começando pela primeira:
Para a segunda equação temos:
Portanto 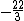 e 4 são as soluções desta equação.
e 4 são as soluções desta equação.

No exemplo anterior havíamos desmembrando a equação modular em duas equações afim, neste exemplo a desmembraremos em duas equações quadráticas:
Vamos solucionar a primeira:
Quais são os números que somados totalizam 6 e que multiplicados produzem 9?
Não há dúvida de que 3 + 3 = 6 e de que 3 . 3 = 9, então segundo as relações de Albert Girard o número 3 são as raízes desta equação.
Agora vamos solucionar a segunda equação:
Calculemos então o discriminante desta equação:
Agora recorrendo à fórmula geral de resolução da equação do segundo grau temos:
Finalmente temos o conjunto solução da equação 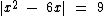 :
:

Neste caso vamos fazer um pouco diferente. Primeiramente vamos substituir |x| por y e encontrarmos as raízes da equação:
O discriminante é igual a 25:
O que nos leva às seguintes raízes:
Como inicialmente havíamos trocado o |x| por y, devemos desfazer a troca.
Para 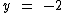 :
:
Como podemos observar, não existe um x real cujo |x| seja igual a -2, pois o módulo de um número real nunca poderá resultar em um número negativo.
Para 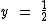 :
:
Logo o conjunto solução da equação 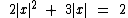 :
:

Solucionarmos esta equação modular precisamos analisar quando 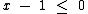 e quando
e quando 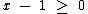 .
.
Quando 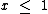 então
então 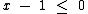 , logo
, logo 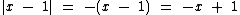 e portanto:
e portanto:
Quando 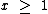 então
então 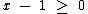 , logo
, logo 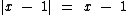 e consequentemente:
e consequentemente:
Concluindo:
Como pudemos observar, cada tipo de equação pode necessitar de um artifício específico para a sua resolução, no entanto em todos os casos precisamos levar em consideração a definição de módulo.
Nenhum comentário:
Postar um comentário