Função Logarítmica

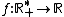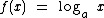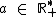Função logarítmica de base a é toda função , definida por  com  e .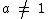

Podemos observar neste tipo de função que a variável independente x é um logaritmando, por isto a denominamos função logarítmica. Observe que a base a é um valor real constante, não é uma variável, mas sim um número real.

A função logarítmica de 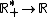 é inversa da função exponencial de  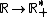e vice-versa, pois:

Representação da Função Logarítmica no Plano Cartesiano

Podemos representar graficamente uma função logarítmica da mesma forma que fizemos com a função exponencial, ou seja, escolhendo alguns valores para x e montando uma tabela com os respectivos valores de f(x). Depois localizamos os pontos no plano cartesiano e traçamos a curva do gráfico.

Vamos representar graficamente a função 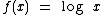 e como estamos trabalhando com um logaritmo de base 10, para simplificar os cálculos vamos escolher para x alguns valores que são potências de 10:

0,001, 0,01, 0,1, 1, 10 e 2.

Temos então seguinte a tabela:

x	y = log x
0,001	y = log 0,001 = -3
0,01	y = log 0,01 = -2
0,1	y = log 0,1 = -1
1	y = log 1 = 0
10	y = log 10 = 1

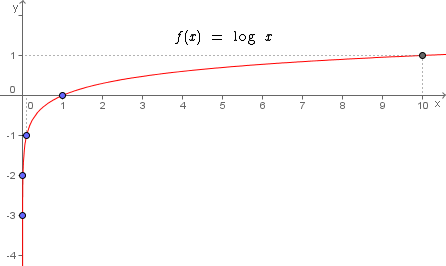
Ao lado temos o gráfico desta função logarítmica, no qual localizamos cada um dos pontos obtidos da tabela e os interligamos através da curva da função:

Veja que para valores de y < 0,01 os pontos estão quase sobre o eixo das ordenadas, mas de fato nunca chegam a estar.

Note também que neste tipo de função uma grande variação no valor de x implica numa variação bem inferior no valor de y.

Por exemplo, se passarmos de x = 100 parax = 1000000, a variação de y será apenas de 2 para 6.

Isto porque:

Função Crescente e Decrescente

Assim como no caso das funções exponenciais, as funções logarítmicas também podem ser classificadas comofunção crescente ou função decrescente.

Isto se dará em função da base a ser maior ou menor que 1. Lembre-se que segundo a definição da função logarítmica 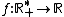, definida por 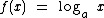, temos qu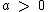e  e .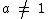

Função Logarítmica Crescente

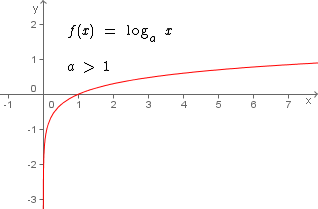
Se 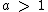 temos uma função logarítmica crescente, qualquer que seja o valor real positivo de x.

No gráfico da função ao lado podemos observar que à medida que x aumenta, também aumenta f(x) ou y. Graficamente vemos que a curva da função é crescente.

Também podemos observar através do gráfico, que para dois valor de x (x₁ e x₂), que 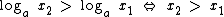, isto para x₁, x₂ e a números reais positivos, com a > 1.

Função Logarítmica Decrescente

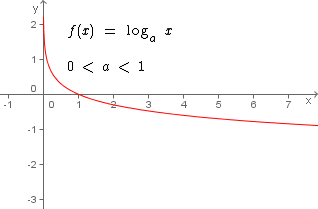
Se 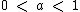 temos uma função logarítmica decrescente em todo o domínio da função.

Neste outro gráfico podemos observar que à medida que xaumenta, y diminui. Graficamente observamos que a curva da função é decrescente.

No gráfico também observamos que para dois valor de x (x₁ ex₂), que 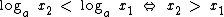, isto para x₁, x₂ e anúmeros reais positivos, com 0 < a < 1.

É importante frisar que independentemente de a função ser crescente ou decrescente, o gráfico da função sempre cruza o eixo das abscissas no ponto (1, 0), além de nunca cruzar o eixo das ordenadas e que o 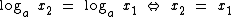, isto para x₁, x₂ e a números reais positivos, com a ≠ 1.