Função Linear

Dentro do estudo das funções já vimos que toda função 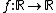 na forma 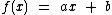, com 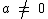 é denominada função afim.

Agora vamos estudar um tipo particular de função afim em que o termo independente de x é igual a zero, isto é, quando 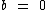. Neste caso particular a denominamos função linear.

Assim sendo, toda função 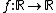 na forma 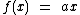, com 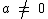 é denominada função linear.

O Gráfico da Função Linear Passa pela Origem do Plano Cartesiano

Uma característica das funções lineares é que o seu gráfico passa pelo ponto(0, 0), a origem do sistema de coordenadas cartesianas.

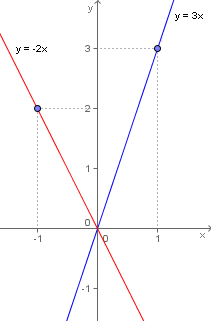
Vamos analisar o gráfico ao lado contendo as funções lineares y = 3x, representado pela reta em azul e y = -2x, representado pela reta em vermelho:

Ambas as funções intersectam o eixo das abscissas exatamente no ponto (0, 0).

Isto ocorre pois o seu coeficiente linear, b, é igual a zero.

É o valor do coeficiente b que determina a ordenada (y) do ponto com abscissa(x) igual a zero.

Para a função y = -2x, quando x = -1 temos que y = 2, representado pelo ponto(-1, 2):

Para a função y = 3x, quando x = 1 temos que y = 3, que representamos pelo ponto (1, 3):

Proporcionalidade na Função Linear

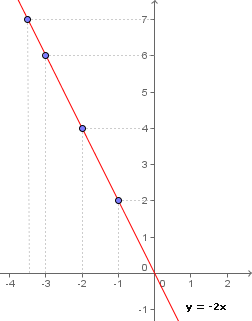
Analisemos ao lado novamente o gráfico da função y = -2x, onde destacamos os pontos (-1, 2), (-2, 4), (-3, 6) e (-⁷/₂, 7):

Como vimos na página sobre grandezas proporcionais, "duas grandezas são diretamente proporcionais quando ao aumentarmos o valor de uma delas um certo número de vezes, o respectivo valor da outra grandeza igualmente aumenta o mesmo número de vezes. Quando diminuímos o valor de uma delas, proporcionalmente o respectivo valor da outra também diminui".

Tendo isto em mente vamos analisar os pontos (-1, 2) e (-2, 4)pertencentes a função.

Observe que se multiplicarmos tanto a abscissa -1 do primeiro ponto, quanto a sua ordenada 2 pelo mesmo valor 2, iremos obter exatamente o ponto (-2, 4).

Se tomarmos os pontos (-1, 2) e (-⁷/₂, 7) e realizarmos os mesmos procedimentos, só que agora multiplicando por 3,5, novamente iremos obter o segundo ponto.

O mesmo ocorrerá se pegarmos, por exemplo, os pontos (-2, 4) e (-3, 6), onde a razão entras as abscissas é igual a razão das ordenadas:

Note que temos uma proporção.

Isto ocorre pois dado um ponto qualquer (x, y) pertencente a função, se multiplicarmos x e y por uma mesma constante k, iremos encontrar o ponto (kx, ky) que também pertence à função.

Quando aumentamos ou diminuímos x um número de k vezes, o valor de y será igualmente aumentado ou diminuído este mesmo número de vezes, portanto k é a constante de proporcionalidade.

Função Identidade

Qualquer função 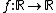 na forma 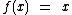, ou seja, uma função afim com 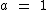e 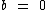 é denominada função identidade.

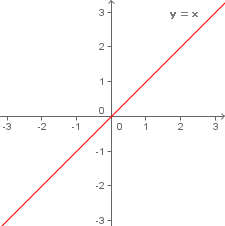
Ao lado temos o gráfico da função identidade no sistema de coordenadas cartesianas:

Podemos observar que a reta que representa a função é formada pelas bissetrizes do 1° e 3° quadrantes.

Em uma função identidade todos os elementos do domínio terão como imagem um elemento com o mesmo valor do elemento no domínio, pois y sempre será igual a x.